Month: November 2021

Statistics basic: stddev and z-score

I’ve been trying to wrap my head around some statistics/data science used for dissecting ddos attacks, and came across a couple of new topics that are quite important but rarely explained.

Sources

Z-Scores aan het uitvogelen?

https://www.wiskunde.net/standaarddeviatie

Standard deviation

Standard deviation is a property of a set that describes the spread around the mean.

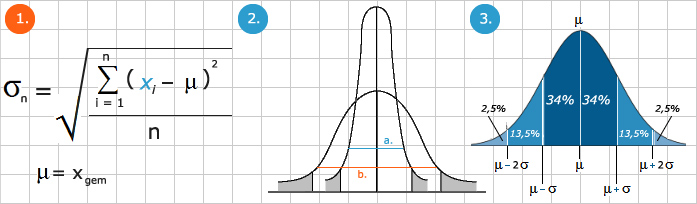
Sx = σ = de standard deviation of the set
Xi = The number i in the set.
Xgem = the mean of the set
Nx = the total number of elements in the set

σ = Sx = √( ∑ ( (xi – xgem)2 / nx) )

Standaarddeviatie
SRC: wiskunde.net

Z-score

z-score: easy normalized way of seeing if something is above the average or below, and if it is an outlier (z-score >3 | <3 is often seen as a outlier)

Z = frac{X - mu}{sigma}.
SRC: statistiekbegleider

mean = average
Z-score = (Measurement – mean) / stddev

In python:

df['zscore'] = ((df['count'] - df['count'].mean()) / df['count'].std(ddof=0)).round().fillna(NONE)

Extra: Newton Binomial

{\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}}

if we take n = 10 and k = 3 (also called 10 choose 3). We will find the outcome to be 120.

The newton Binomial is used to find the number of ways to choose k (three) elements out of n (10). Take for example the amount of combinations of toppings you can choose on a pizza when you can choose at most 3 from a total pool of 10 options.